Текст задания

3.1 Работа машины Тьюринга описана следующей функциональной схемой:

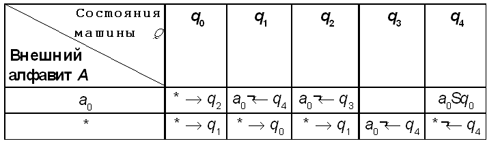
Определите, какое сообщение будет на ленте после окончания работы машины, и укажите (например, * над ячейкой), напротив какой ячейки в этот момент будет находиться ее пишущий блок.

3.2 На ленте машины Тьюринга записана строка, состоящая из символов “*” и символов “#” (вперемежку без пробелов). Один из возможных вариантов такой строки приведен на рис. 2.

Рис. 2

Для приведенной ниже функциональной схемы определите, для решения какой задачи она предназначена. В качестве ответа укажите закономерность, связывающую исходную последовательность с результирующей.

3.3 В задании 8 из раздела "Вопросы и задания" Параграфа 2 Лекция 2 (стр. 46) машина Тьюринга удаляет из исходного сообщения все знаки "+". Проанализировав программу МТ, заданную в виде таблицы, укажите, что выполняет эта машина Тьюринга в каждом состоянии.

Задания 3.4-3.5 будут проверяться тестированием на имитаторе машины Тьюринга "Алго2000" с помощью системы тестов. Сумма баллов по всем тестам одного задания равна 5. Считается, что на ленте первоначальная информация записана корректно (т.к. в точности соответствует условию). Количество внутренних состояний - на усмотрение решающего задачу.

3.4 На ленте записана последовательность из n символов “*” (n – натуральное число). Составьте функциональную схему для машины Тьюринга, с помощью которой на ленте вместо исходной последовательности будет записана последовательность из n/2 звездочек. (Все звездочки в выходном слове записаны непрерывно, без пробелов.)

Пусть внешний алфавит состоит из символа “a0”, цифр 0, 1, 2, ..., 9, а также символов “+” и “=”. На ленту записан пример на сложение двух натуральных чисел в десятичной системе счисления. Образец:

Составьте функциональную схему для машины Тьюринга, с помощью которой на ленте будет записана сумма этих чисел. Ответ требуется записать после знака “=”.

Решение

Решение контрольной работы оформлено в виде архива, который содержит отчет в Word по заданиям 3.1-3.3 и файлы с программами, созданные в программе-имитаторе машины Тьюринга "Алго2000" для заданий 3.3-3.4. Для получения решения необходимо оформить заказ и оплатить его.