Текст задания

Можно закупить корм двух видов (I и II). В каждой единице корма I вида содержатся 1 ед. витамина А, 2 ед. витамина В и нет витамина С; в каждой единице корма II вида – 2 ед. витамина А, 1 ед. витамина В и 1 ед. витамина С. Животному необходимо дать в сутки не менее 10 ед. витамина А, 10 ед. витамина В и 4 ед. витамина С. Составить наиболее дешевый рацион питания животного, если стоимость единицы корма I вида равна 2 ден. ед., а стоимость единицы корма II вида – 5 ден. ед.

Решение

Пусть x1 – закупаемое количество единиц корма I вида, а x2 – Закупаемое количество единиц корма II вида, тогда можно составить систему ограничений для данной задачи:

x1+2x2≥10,

2x1+x2≥10,

x2≥4,

x1≥0,

x2≥0.

Учитывая стоимость единицы корма каждого вида целевая функция примет вид:

F=2x1+5x2→min

Решим данную задачу линейного программирования графическим методом.

Построим область допустимых решений, т.е. решим графически систему неравенств. Для этого построим каждую прямую и определим полуплоскости, заданные неравенствами (полуплоскости обозначены штрихом).

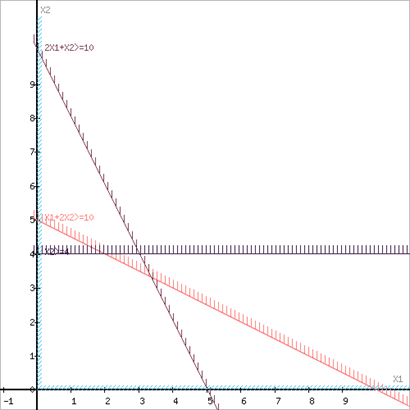
или

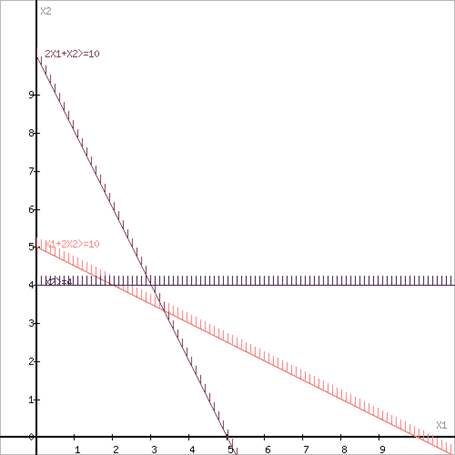
Границы области допустимых решений

Пересечением полуплоскостей будет являться область, координаты точек которого удовлетворяют условию неравенствам системы ограничений задачи.

Обозначим границы области многоугольника решений.

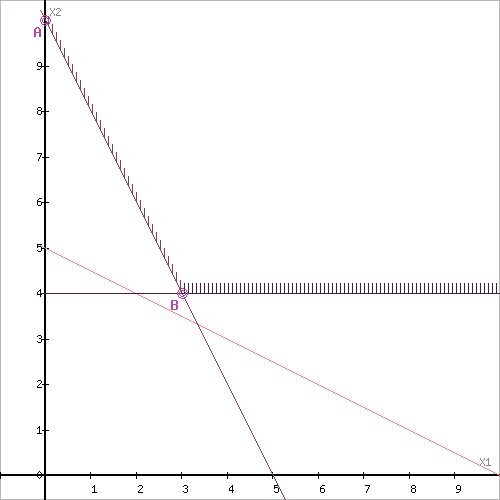
Рассмотрим целевую функцию задачи F = 2x1+5x2 → min. 

Построим прямую, отвечающую значению функции F = 0: F = 2x1+5x2 = 0. Вектор-градиент, составленный из коэффициентов целевой функции, указывает направление минимизации F(X). Начало вектора – точка (0; 0), конец – точка (2; 5). Будем двигать эту прямую параллельным образом. Поскольку нас интересует минимальное решение, поэтому двигаем прямую до первого касания обозначенной области. На графике эта прямая обозначена пунктирной линией.

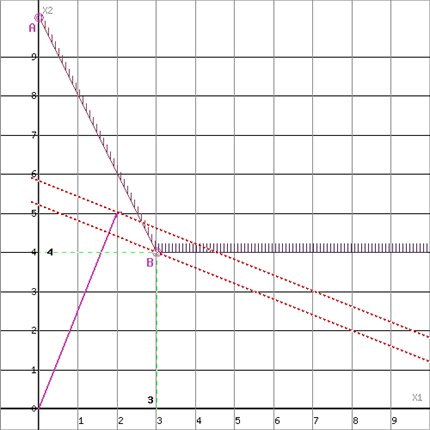
Равный масштаб

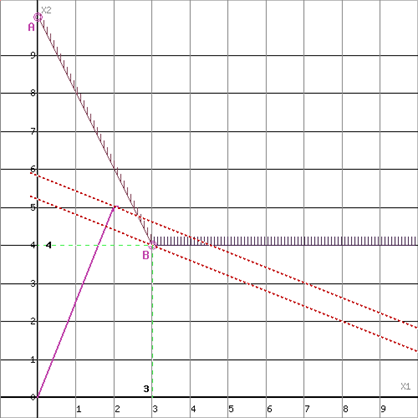
Область допустимых решений представляет собой одну точку.

Прямая F(x) = const пересекает область в точке B. Так как точка B получена в результате пересечения прямых(2) и (3), то ее координаты удовлетворяют уравнениям этих прямых:

2x1+x2≥10

x2≥4

Решив систему уравнений, получим: x1 = 3, x2 = 4

Откуда найдем минимальное значение целевой функции:

F(X) = 2*3 + 5*4 = 26